Raamistik
CNV-sid tuvastatakse geeniandmete pealt, kasutades näiteks PennCNV algoritmi. See ei ole aga kunagi täiesti täpne. Algoritmi vigade mõju vähendamiseks on Tartu Ülikooli Eesti Geenivaramus (TÜ EGVs) välja töötatud CNV kvaliteediskoor.
Antud töös ehitasime teoreetilise raamistiku erinevate CNV tunnuste hindamiseks ning esimest korda näitasime, et kvaliteediskoor tõesti aitab PennCNV algoritmi poolt tehtud vigu parandada.
Simulatsioonide raamistik
Loodud raamistiku võtab kokku alljärgnev joonis, kuid selle järel toome ka põhjalikuma matemaatilise käsitluse.
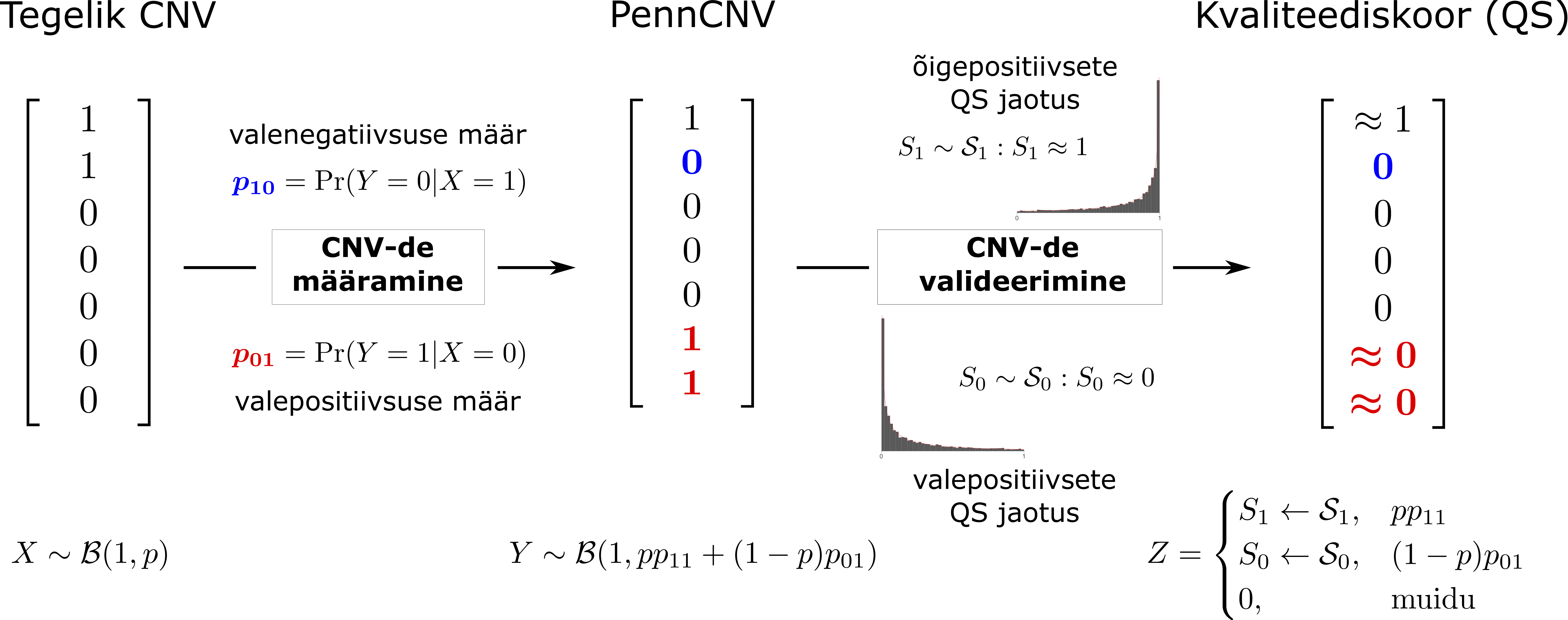
Tegelik CNV tunnus
Olgu \(X\sim \mathcal{B}(1, p)\) tegeliku CNV esinemist kirjeldav juhuslik suurus, kus \(p\) on CNV suhteline sagedus uuritavas populatsioonis.
PennCNV tunnus
Olgu \(Y=f(X)\) juhuslik suurus, mis tähistab PennCNV poolt määratud CNV-d ning olgu PennCNV meetodi valepositiivsuse määr \[p_{01} = P(Y=1|X=0)\] ning valenegatiivsuse määr \[p_{10} = P(Y=0|X=1).\] Siis õige-positiivsete ja õige-negatiivsete tulemuste määrad on vastavalt \(p_{11}=1-p_{10}\) ning \(p_{00}=1-p_{01}\). Tuleneb, et \[Y \sim \mathcal{B}\left(1, pp_{11}+(1-p)p_{01}\right),\] kus CNV-de suhteline sagedus on tegeliku CNV tunnusega võrreldes muutunud.
Kvaliteediskoor
Kvaliteediskoor on arv lõigust [0,1], mis määratakse igale PennCNV poolt määratud CNV-le eesmärgiga korrigeerida valepositiivsed leiud. Seega ideaalis peaksid kõik valepositiivsed CNV-d saama skoori, mis on 0 lähedal, ja õigepositiivsed CNV-d skoori, mis on 1 lähedal.
Olgu \(X\) ja \(Y\) defineeritud nii nagu eelnevalt. Olgu \(Z=g(X,Y)\) kvaliteediskoori kirjeldav juhuslik suurus ja \(\mathcal{S}_0\) ning \(\mathcal{S}_1\) tundmatud jaotused, millest on genereeritud vastavalt valepositiivsete ja õigepositiivsete CNV leidude kvaliteediskoorid.
Siis \[Z=g(X,Y)= \begin{cases}\\[-30pt] S_1\leftarrow \mathcal{S}_1, & X=1\land Y=1\\[-5pt] S_0\leftarrow \mathcal{S}_0, & X=0\land Y=1\\[-5pt] 0, & \text{muidu} \end{cases} = \begin{cases}\\[-30pt] S_1\leftarrow \mathcal{S}_1, & \text{tõenäosusega } pp_{11}\\[-5pt] S_0\leftarrow \mathcal{S}_0, & \text{tõenäosusega } (1-p)p_{01}\\[-5pt] 0, & \text{muidu,} \end{cases} \]
kus tähistus \(S_i\leftarrow \mathcal{S}_i\enspace(i=0, 1)\) märgib juhusliku suuruse \(S_i\) valimist jaotusest \(\mathcal{S}_i\).
Valepositiivsuse ja -negatiivsuse määrad on hinnatud TÜ EGV andmete põhjal. Sarnaselt on jaotused \(\mathcal{S}_0\) ja \(\mathcal{S}_1\) hinnatud sõltumatutest bioloogilistest TÜ EGV andmetest.
Miks kvaliteediskoor töötab?
Kvaliteediskoor suudab ümber pöörata PennCNV algoritmi poolt hinnatud valepositiivseid CNV-sid. Seda on visualiseeritud alljärgneva animatsiooniga, mis näitab, kuidas regressioonisirge tõus muutub erinevate CNV tunnuste kasutamisel.
- Esimeses (initsialiseerimise) faasis kuvatakse kõik vaatlused.
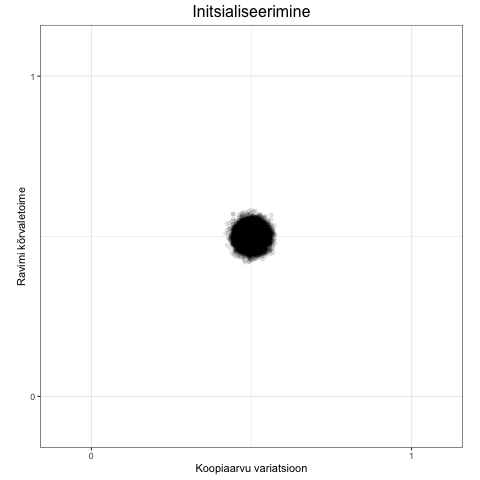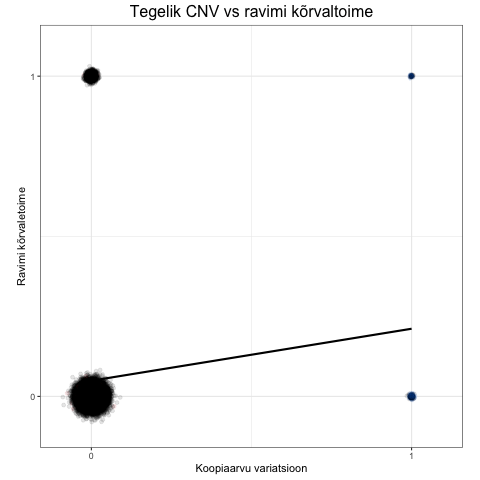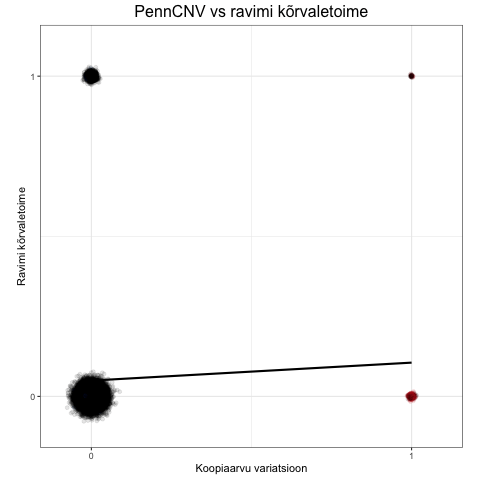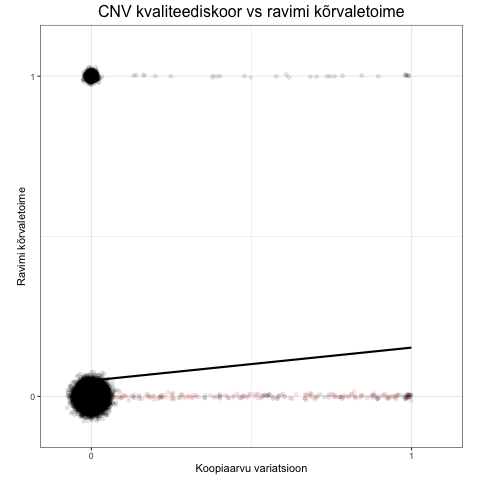
- Teises faasis kuvatakse regressioonisirge eeldusel, et meil on kõikide vaatluste kohta teada tegelik CNV olemasolu.
- Kolmandas faasis kuvatakse regressioonisirge PennCNV tunnuse korral. Punased punktid viitavad siin valepositiivsetele ja sinised valenegatiivsetele. Paneme tähele, et regressioonisirge langeb, mis viitabki vähenenud efektile CNV tunnuse ja ravimi kõrvaltoime vahel.
- Neljandas faasis kuvatakse regressioonisirge CNV kvaliteediskoori korral. Punased punktid viitavad jällegi valepositiivsetele, mis suures osas tagasi pööratakse. Regressioonisirge tõuseb, sest juhtude hulgas on 1) tegelikke CNV kandjaid rohkem ja 2) valepositiivseid vähem (tulenevalt juhtude harvast esinemisest), mistõttu on tagasipööramisi juhtude hulgas vähem.
Simuleerimine
Olgu \(n_0\) ja \(n_1\) vastavalt kontrollide ja juhtude arv valimis ning \(p_0\) ja \(p_1\) CNV-de osakaal vastavalt kontrollide ja juhtude seas (kas tegelik osakaal või PennCNV tunnuse osakaal).
Simuleerimine binaarse tunnuse korral
Olgu \(X_{0,i}\sim\mathcal{B}(1, p_0), i=1,\ldots, n_0\) ja \(X_{1,j}\sim\mathcal{B}(1, p_1), j=1,\ldots, n_1\) sõltumatud juhuslikud suurused, mis tähistavad CNV esinemist vastavalt kontrollide ja juhtude seas. Siis CNV-de arvud on vastavalt kontrollidel \[T_0=\sum_{i=1}^{n_0}X_{0,i}\sim\mathcal{B}(n_0, p_0)\] ja juhtudel
\[T_1=\sum_{j=1}^{n_1}X_{1,j}\sim\mathcal{B}(n_1, p_1).\]
Olgu \(\alpha\) maksimaalne lubatav I liiki vea tõenäosus. Siis võimsuse (tegelikult kehtiva sisuka hüpoteesi vastuvõtmise tõenäosus) saab arvutada valemiga
\[\text{võimsus}=P(P_t<\alpha|p_0\ne p_1)=\sum_{i=1}^{n_0}\sum_{j=1}^{n_1}P(T_0=i, T_1=j | p_0 \ne p_1)\cdot I(P_{t,i,j}<\alpha),\]
kus \(P_t\) tähistab statistilise testi \(t\) (näiteks logistilise regressiooni puhul Waldi testi) p-väärtuste jaotusega juhuslikku suurust konkreetse simulatsiooni konfiguratsiooni \((n_0,n_1,p_0,p_1)\) korral, \(P_{t,i,j}\) on testi \(t\) p-väärtus \(T_0=i\) ja \(T_1=j\) korral ning \(I\) on indikaatorfunktsioon. Juhul kui \(p_0=p_1\), saab eelneva valemi abil arvutada I liiki vea tõenäosuse.
Eeldades, et CNV kandjad juhtude ja kontrollide seas on sõltumatud, saab iga paari \((i, j)\) korral arvutada \[P(T_0=i, T_1=j)=P(T_0=i)P(T_1=j)=\mathrm{C}_{n_0}^ip_0^i(1-p_0)^{n_0-i}\cdot \mathrm{C}_{n_1}^jp_1^j(1-p_1)^{n_1-j}.\]
Simuleerimine kvaliteediskoori korral
Olgu \(\forall i \in \{1, \ldots n_0\}\) korral \[Z_{0,i}= \begin{cases} S_1\leftarrow \mathcal{S}_1, & p_0p_{11}\\[-5pt] S_0\leftarrow \mathcal{S}_0, & (1-p_0)p_{01}\\[-5pt] 0, & \text{muidu} \end{cases}\] ning \(\forall j \in \{1, \ldots n_1\}\) korral \[ Z_{1,j}= \begin{cases} S_1\leftarrow \mathcal{S}_1, & p_1p_{11}\\[-5pt] S_0\leftarrow \mathcal{S}_0, & (1-p_1)p_{01}\\[-5pt] 0, & \text{muidu.} \end{cases} \]
Siis tuleb iga genereeritud valimi jaoks läbi viia statistiline analüüs (näiteks logistiline regressioonanalüüs) ning seejärel saab empiirilise võimsuse arvutada kui nende testide osakaalu, mille puhul p-väärtus on väiksem valitud olulisuse nivoost \(\alpha\):
\[\text{võimsus} = P(P_t<\alpha|p_0\ne p_1) = \frac1m\sum_{k=1}^mI(P_{k,t}<\alpha),\]
kus \(P_{k,t}\) on statistilise testi \(t\) p-väärtus \(k\)-nda valimi ja konkreetse simulatsiooni konfiguratsiooni \((n_0,n_1,p_0,p_1)\) korral.